Data Structures
struct	nfsft_wisdom
	Wisdom structure. More...

Macros
#define	BWEXP_MAX 10
#define	BW_MAX 1024
#define	ROW(k) (k*(wisdom.N_MAX+2))
#define	ROWK(k) (k*(wisdom.N_MAX+2)+k)
#define	NFSFT_DEFAULT_NFFT_CUTOFF 6
	The default NFFT cutoff parameter.
#define	NFSFT_DEFAULT_THRESHOLD 1000
	The default threshold for the FPT.
#define	NFSFT_BREAK_EVEN 5
	The break-even bandwidth 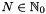$N \in \mathbb{N}_0$ .

Enumerations
enum	bool { false = 0, true = 1 }

Functions
void	alpha_al_row (R *alpha, const int N, const int n)
void	beta_al_row (R *beta, const int N, const int n)
void	gamma_al_row (R *gamma, const int N, const int n)
void	alpha_al_all (R *alpha, const int N)
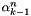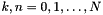	Compute three-term-recurrence coefficients $\alpha_{k-1}^n$ of associated Legendre functions for $k,n = 0,1,\ldots,N$ .
void	beta_al_all (R *beta, const int N)
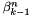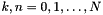	Compute three-term-recurrence coefficients $\beta_{k-1}^n$ of associated Legendre functions for $k,n = 0,1,\ldots,N$ .
void	gamma_al_all (R *gamma, const int N)
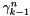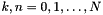	Compute three-term-recurrence coefficients $\gamma_{k-1}^n$ of associated Legendre functions for $k,n = 0,1,\ldots,N$ .
void	eval_al (R x, R y, const int size, const int k, R alpha, R beta, R *gamma)
	Evaluates an associated Legendre polynomials 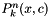using the Clenshaw-algorithm.
int	eval_al_thresh (R x, R y, const int size, const int k, R alpha, R beta, R *gamma, R threshold)
	Evaluates an associated Legendre polynomials 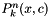using the Clenshaw-algorithm if it no exceeds a given threshold.
static void	c2e (nfsft_plan *plan)
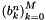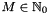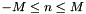	Converts coefficients $\left(b_k^n\right)_{k=0}^M$ with $M \in \mathbb{N}_0$ , $-M \le n \le M$ from a linear combination of Chebyshev polynomials $f(\cos\vartheta) = \sum_{k=0}^{2\lfloor\frac{M}{2}\rfloor} a_k (\sin\vartheta)^{n\;\mathrm{mod}\;2} T_k(\cos\vartheta)$ to coefficients $\left(c_k^n\right)_{k=0}^M$ matching the representation by complex exponentials $f(\cos\vartheta) = \sum_{k=-M}^{M} c_k \mathrm{e}^{\mathrm{i}k\vartheta}$ for each order $n=-M,\ldots,M$ .
static void	c2e_transposed (nfsft_plan *plan)
	Transposed version of the function c2e.
void	nfsft_init (nfsft_plan *plan, int N, int M)
void	nfsft_init_advanced (nfsft_plan *plan, int N, int M, unsigned int flags)
void	nfsft_init_guru (nfsft_plan *plan, int N, int M, unsigned int flags, unsigned int nfft_flags, int nfft_cutoff)
void	nfsft_precompute (int N, double kappa, unsigned int nfsft_flags, unsigned int fpt_flags)
void	nfsft_forget (void)
void	nfsft_finalize (nfsft_plan *plan)
void	nfsft_trafo_direct (nfsft_plan *plan)
void	nfsft_adjoint_direct (nfsft_plan *plan)
void	nfsft_trafo (nfsft_plan *plan)
void	nfsft_adjoint (nfsft_plan *plan)
void	nfsft_precompute_x (nfsft_plan *plan)

Variables
static struct nfsft_wisdom	wisdom = {false,0U,-1,-1,0,0,0,0,0}
	The global wisdom structure for precomputed data.

Detailed Description

Macro Definition Documentation

#define NFSFT_DEFAULT_NFFT_CUTOFF 6

The default NFFT cutoff parameter.

Author:: Jens Keiner

Definition at line 65 of file nfsft.c.

#define NFSFT_DEFAULT_THRESHOLD 1000

The default threshold for the FPT.

Author:: Jens Keiner

Definition at line 72 of file nfsft.c.

#define NFSFT_BREAK_EVEN 5

The break-even bandwidth $N \in \mathbb{N}_0$ .

Author:: Jens Keiner

Definition at line 79 of file nfsft.c.

Function Documentation

void alpha_al_all	(	R *	alpha,
		const int	N
	)

inline

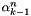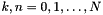Compute three-term-recurrence coefficients $\alpha_{k-1}^n$ of associated Legendre functions for $k,n = 0,1,\ldots,N$ .

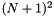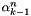alpha A pointer to an array of doubles of size where the coefficients will be stored such that alpha[n+(N+1)+k] = $\alpha_{k-1}^n$ .
N The upper bound .

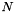Definition at line 91 of file legendre.c.

void beta_al_all	(	R *	beta,
		const int	N
	)

inline

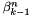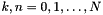Compute three-term-recurrence coefficients $\beta_{k-1}^n$ of associated Legendre functions for $k,n = 0,1,\ldots,N$ .

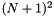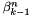beta A pointer to an array of doubles of size where the coefficients will be stored such that beta[n+(N+1)+k] = $\beta_{k-1}^n$ .
N The upper bound .

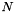Definition at line 100 of file legendre.c.

void gamma_al_all	(	R *	gamma,
		const int	N
	)

inline

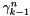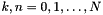Compute three-term-recurrence coefficients $\gamma_{k-1}^n$ of associated Legendre functions for $k,n = 0,1,\ldots,N$ .

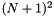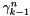beta A pointer to an array of doubles of size where the coefficients will be stored such that gamma[n+(N+1)+k] = $\gamma_{k-1}^n$ .
N The upper bound .

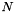Definition at line 109 of file legendre.c.

void eval_al	(	R *	x,
		R *	y,
		const int	size,
		const int	k,
		R *	alpha,
		R *	beta,
		R *	gamma
	)

Evaluates an associated Legendre polynomials 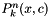$P_k^n(x,c)$ using the Clenshaw-algorithm.

x A pointer to an array of nodes where the function is to be evaluated
y A pointer to an array where the function values are returned
size The length of x and y
k The index
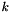
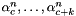
alpha A pointer to an array containing the recurrence coefficients $\alpha_c^n,\ldots,\alpha_{c+k}^n$
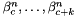
beta A pointer to an array containing the recurrence coefficients $\beta_c^n,\ldots,\beta_{c+k}^n$
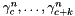
gamma A pointer to an array containing the recurrence coefficients $\gamma_c^n,\ldots,\gamma_{c+k}^n$

Definition at line 118 of file legendre.c.

int eval_al_thresh	(	R *	x,
		R *	y,
		const int	size,
		const int	k,
		R *	alpha,
		R *	beta,
		R *	gamma,
		R	threshold
	)

Evaluates an associated Legendre polynomials 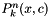$P_k^n(x,c)$ using the Clenshaw-algorithm if it no exceeds a given threshold.

x A pointer to an array of nodes where the function is to be evaluated
y A pointer to an array where the function values are returned
size The length of x and y
k The index
alpha A pointer to an array containing the recurrence coefficients $\alpha_c^n,\ldots,\alpha_{c+k}^n$
beta A pointer to an array containing the recurrence coefficients $\beta_c^n,\ldots,\beta_{c+k}^n$
gamma A pointer to an array containing the recurrence coefficients $\gamma_c^n,\ldots,\gamma_{c+k}^n$
threshold The threshold

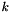
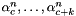
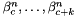
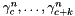
Definition at line 163 of file legendre.c.

static void c2e ( nfsft_plan * plan )

inlinestatic

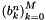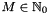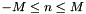Converts coefficients $\left(b_k^n\right)_{k=0}^M$ with $M \in \mathbb{N}_0$ , $-M \le n \le M$ from a linear combination of Chebyshev polynomials

$f(\cos\vartheta) = \sum_{k=0}^{2\lfloor\frac{M}{2}\rfloor} a_k (\sin\vartheta)^{n\;\mathrm{mod}\;2} T_k(\cos\vartheta)$

to coefficients 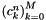$\left(c_k^n\right)_{k=0}^M$ matching the representation by complex exponentials

$f(\cos\vartheta) = \sum_{k=-M}^{M} c_k \mathrm{e}^{\mathrm{i}k\vartheta}$

for each order 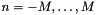$n=-M,\ldots,M$ .

plan The nfsft_plan containing the coefficients 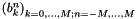$\left(b_k^n\right)_{k=0,\ldots,M;n=-M,\ldots,M}$

Remarks:: The transformation is computed in place.

Author:: Jens Keiner

Definition at line 111 of file nfsft.c.

References nfsft_plan::f_hat_intern, and nfsft_plan::N.

static void c2e_transposed ( nfsft_plan * plan )

inlinestatic

Transposed version of the function c2e.

plan The nfsft_plan containing the coefficients 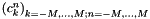$\left(c_k^n\right)_{k=-M,\ldots,M;n=-M,\ldots,M}$

Remarks:: The transformation is computed in place.

Author:: Jens Keiner

Definition at line 189 of file nfsft.c.

References nfsft_plan::f_hat, and nfsft_plan::N.

Variable Documentation

struct nfsft_wisdom wisdom = {false,0U,-1,-1,0,0,0,0,0}

static

The global wisdom structure for precomputed data.

wisdom.initialized is set to false and wisdom.flags is set to 0U.

Author:: Jens Keiner

Definition at line 87 of file nfsft.c.

Data Structures

Macros

Enumerations

Functions

Variables

Detailed Description

Macro Definition Documentation

Function Documentation

Variable Documentation