

|
3.2.3 |
Include header for FFTW3 library for its complex type. More...
Macros | |
| #define | NFFT_SWAP_complex(x, y) |
| Swapping of two vectors. | |
| #define | NFFT_SWAP_double(x, y) |
| Swapping of two vectors. | |
| #define | PI 3.141592653589793238462643383279502884197169399375105820974944592 |
| Formerly known to be an irrational number. | |
| #define | PI2 6.283185307179586476925286766559005768394338798750211641949889185 |
| #define | PI4 12.56637061435917295385057353311801153678867759750042328389977837 |
| #define | NFFT_MAX(a, b) ((a)>(b)? (a) : (b)) |
| Maximum of its two arguments. | |
| #define | NFFT_MIN(a, b) ((a)<(b)? (a) : (b)) |
| Mimimum of its two arguments. | |
Functions | |
| double | nfft_bspline_old (int k, double x, double *A) |
| To test the new one. | |
| double | nfft_bspline (int k, double x, double *scratch) |
Computes the B-spline 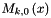 , scratch is used for de Boor's scheme. , scratch is used for de Boor's scheme. | |
| int | nfft_prod_int (int *vec, int d) |
Computes integer 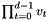 . . | |
| int | nfst_prod_minus_a_int (int *vec, int a, int d) |
Computes integer 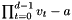 . . | |
| int | nfft_plain_loop (int *idx, int *N, int d) |
Computes 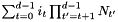 . . | |
| double | nfft_prod_real (double *vec, int d) |
Computes double 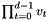 . . | |
| double | nfft_dot_complex (fftw_complex *x, int n) |
Computes the inner/dot product 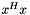 . . | |
| double | nfft_dot_double (double *x, int n) |
Computes the inner/dot product 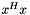 . . | |
| double | nfft_dot_w_complex (fftw_complex *x, double *w, int n) |
Computes the weighted inner/dot product 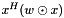 . . | |
| double | nfft_dot_w_double (double *x, double *w, int n) |
Computes the weighted inner/dot product 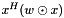 . . | |
| double | nfft_dot_w_w2_complex (fftw_complex *x, double *w, double *w2, int n) |
Computes the weighted inner/dot product 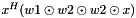 . . | |
| double | nfft_dot_w2_complex (fftw_complex *x, double *w2, int n) |
Computes the weighted inner/dot product 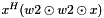 . . | |
| void | nfft_cp_complex (fftw_complex *x, fftw_complex *y, int n) |
Copies 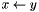 . . | |
| void | nfft_cp_double (double *x, double *y, int n) |
Copies 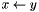 . . | |
| void | nfft_cp_a_complex (fftw_complex *x, double a, fftw_complex *y, int n) |
Copies  . . | |
| void | nfft_cp_a_double (double *x, double a, double *y, int n) |
Copies  . . | |
| void | nfft_cp_w_complex (fftw_complex *x, double *w, fftw_complex *y, int n) |
Copies 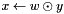 . . | |
| void | nfft_cp_w_double (double *x, double *w, double *y, int n) |
Copies 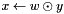 . . | |
| void | nfft_upd_axpy_complex (fftw_complex *x, double a, fftw_complex *y, int n) |
Updates 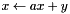 . . | |
| void | nfft_upd_axpy_double (double *x, double a, double *y, int n) |
Updates 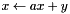 . . | |
| void | nfft_upd_xpay_complex (fftw_complex *x, double a, fftw_complex *y, int n) |
Updates 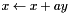 . . | |
| void | nfft_upd_xpay_double (double *x, double a, double *y, int n) |
Updates 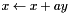 . . | |
| void | nfft_upd_axpby_complex (fftw_complex *x, double a, fftw_complex *y, double b, int n) |
Updates 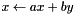 . . | |
| void | nfft_upd_axpby_double (double *x, double a, double *y, double b, int n) |
Updates 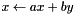 . . | |
| void | nfft_upd_xpawy_complex (fftw_complex *x, double a, double *w, fftw_complex *y, int n) |
Updates 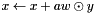 . . | |
| void | nfft_upd_xpawy_double (double *x, double a, double *w, double *y, int n) |
Updates 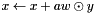 . . | |
| void | nfft_upd_axpwy_complex (fftw_complex *x, double a, double *w, fftw_complex *y, int n) |
Updates 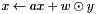 . . | |
| void | nfft_upd_axpwy_double (double *x, double a, double *w, double *y, int n) |
Updates 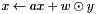 . . | |
| void | nfft_fftshift_complex (fftw_complex *x, int d, int *N) |
| Swaps each half over N[d]/2. | |
| void | nfft_vpr_int (int *x, int n, char *text) |
| Prints a vector of integer numbers. | |
| void | nfft_vpr_double (double *x, int n, const char *text) |
| Prints a vector of doubles numbers. | |
| void | nfft_vpr_complex (fftw_complex *x, int n, const char *text) |
| Prints a vector of complex numbers. | |
| void | nfft_vrand_unit_complex (fftw_complex *x, int n) |
Inits a vector of random complex numbers in ![$[0,1]\times[0,1]{\rm i}$](form_25.png) . . | |
| void | nfft_vrand_shifted_unit_double (double *x, int n) |
Inits a vector of random double numbers in ![$[-1/2,1/2]$](form_26.png) . . | |
| void | nfft_voronoi_weights_1d (double *w, double *x, int M) |
Computes non periodic voronoi weights, assumes ordered nodes 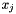 . . | |
| void | nfft_voronoi_weights_S2 (double *w, double *xi, int M) |
| Computes voronoi weights for nodes on the sphere S^2. | |
| double | nfft_modified_fejer (int N, int kk) |
Computes the damping factor for the modified Fejer kernel, ie 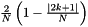 . . | |
| double | nfft_modified_jackson2 (int N, int kk) |
| Computes the damping factor for the modified Jackson kernel. | |
| double | nfft_modified_jackson4 (int N, int kk) |
| Computes the damping factor for the modified generalised Jackson kernel. | |
| double | nfft_modified_sobolev (double mu, int kk) |
| Computes the damping factor for the modified Sobolev kernel. | |
| double | nfft_modified_multiquadric (double mu, double c, int kk) |
| Computes the damping factor for the modified multiquadric kernel. | |
| int | nfft_smbi (const double x, const double alpha, const int nb, const int ize, double *b) |
Calculates the modified bessel function 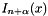 , possibly scaled by , possibly scaled by 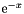 , for real non-negative , for real non-negative 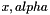 with with 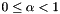 , and , and  . . | |
| double | nfft_drand48 (void) |
| void | nfft_srand48 (long int seed) |
| void | nfft_sort_node_indices_radix_lsdf (int n, int *keys0, int *keys1, int rhigh) |
| Radix sort for node indices. | |
| void | nfft_sort_node_indices_radix_msdf (int n, int *keys0, int *keys1, int rhigh) |
| Radix sort for node indices. | |
| int | nfft_get_num_threads (void) |
Include header for FFTW3 library for its complex type.
This module implements frequently used utility functions. In particular, this includes simple measurement of resources, evaluation of window functions, vector routines for basic linear algebra tasks, and computation of weights for the inverse transforms.
| #define NFFT_SWAP_complex | ( | x, | |
| y | |||
| ) |
Swapping of two vectors.
Definition at line 52 of file nfft3util.h.
Referenced by fgt_test_andersson(), fgt_test_error(), fgt_test_error_p(), fgt_test_simple(), glacier_cv(), main(), solver_loop_one_step_cgnr_complex(), solver_loop_one_step_landweber_complex(), solver_loop_one_step_steepest_descent_complex(), and taylor_time_accuracy().
| #define NFFT_SWAP_double | ( | x, | |
| y | |||
| ) |
Swapping of two vectors.
Definition at line 57 of file nfft3util.h.
Referenced by solver_loop_one_step_cgnr_double(), solver_loop_one_step_landweber_double(), and solver_loop_one_step_steepest_descent_double().
| void nfft_voronoi_weights_S2 | ( | double * | w, |
| double * | xi, | ||
| int | M | ||
| ) |
Computes voronoi weights for nodes on the sphere S^2.
Definition at line 581 of file util.c.
References nfft_free(), nfft_malloc(), and PI.
Referenced by main().
| int nfft_smbi | ( | const R | x, |
| const R | alpha, | ||
| const int | nb, | ||
| const int | ize, | ||
| R * | b | ||
| ) |
Calculates the modified bessel function 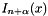 , possibly scaled by
, possibly scaled by 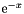 , for real non-negative
, for real non-negative 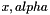 with
with 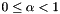 , and
, and  .
.
x non-negative real number in 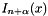
alpha non-negative real number with 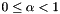 in
in 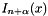
nb number of functions to be calculated ize switch between no scaling (ize = 1) and exponential scaling (ize = 2) b real output vector to contain 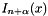 ,
, 
nb, then all values in b have been calculated to full accuracy. If not, errors are indicated using the following scheme: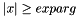 ). In this case, the output vector b is not calculated and
). In this case, the output vector b is not calculated and ncalc is set to 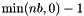 .
.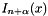 are calculated to full accuracy for
are calculated to full accuracy for 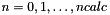 . The rest of the values up to
. The rest of the values up to  is calculated to a lower accuracy.
is calculated to a lower accuracy.This program is based on a program written by David J. Sookne [2] that computes values of the Bessel functions 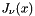 or
or 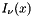 for real argument
for real argument 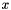 and integer order
and integer order 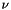 . modifications include the restriction of the computation to the Bessel function
. modifications include the restriction of the computation to the Bessel function 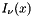 for non-negative real argument, the extension of the computation to arbitrary non-negative orders
for non-negative real argument, the extension of the computation to arbitrary non-negative orders 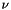 , and the elimination of most underflow.
, and the elimination of most underflow.
References: [1] F. W. J. Olver and D. J. Sookne, A note on backward recurrence algorithms", Math. Comput. (26), 1972, pp 125 – 132. [2] D. J. Sookne, "Bessel functions of real argument and int order", NBS Jour. of Res. B. (77B), 1973, pp. 125 – 132.
Modified by W. J. Cody, Applied Mathematics Division, Argonne National Laboratory, Argonne, IL, 60439, USA
Modified by Jens Keiner, Institute of Mathematics, University of Lübeck, 23560 Lübeck, Germany
Definition at line 950 of file util.c.
References nfsft_wisdom::alpha.
Referenced by main().
| void nfft_sort_node_indices_radix_lsdf | ( | int | n, |
| int * | keys0, | ||
| int * | keys1, | ||
| int | rhigh | ||
| ) |
| void nfft_sort_node_indices_radix_msdf | ( | int | n, |
| int * | keys0, | ||
| int * | keys1, | ||
| int | rhigh | ||
| ) |
Radix sort for node indices.
Radix sort for node indices.
Definition at line 1383 of file util.c.
References nfft_sort_node_indices_radix_msdf().
Referenced by nfft_sort_node_indices_radix_msdf().