

|
3.2.3 |
Functions | |
| static int | polar_grid (int T, int R, double *x, double *w) |
Generates the points 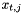 with weights with weights 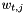 for the polar grid with for the polar grid with 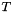 angles and angles and 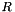 offsets. offsets. | |
| static int | polar_dft (fftw_complex *f_hat, int NN, fftw_complex *f, int T, int R, int m) |
| discrete polar FFT | |
| static int | polar_fft (fftw_complex *f_hat, int NN, fftw_complex *f, int T, int R, int m) |
| NFFT-based polar FFT. | |
| static int | inverse_polar_fft (fftw_complex *f, int T, int R, fftw_complex *f_hat, int NN, int max_i, int m) |
| inverse NFFT-based polar FFT | |
| int | main (int argc, char **argv) |
| test program for various parameters | |
|
static |
Generates the points 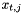 with weights
with weights 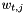 for the polar grid with
for the polar grid with 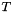 angles and
angles and 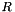 offsets.
offsets.
The nodes of the polar grid lie on concentric circles around the origin. They are given for 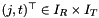 by a signed radius
by a signed radius 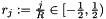 and an angle
and an angle 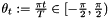 as
as
![\[ x_{t,j} := r_j\left(\cos\theta_t, \sin\theta_t\right)^{\top}\,. \]](form_126.png)
The total number of nodes is 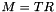 , whereas the origin is included multiple times.
, whereas the origin is included multiple times.
Weights are introduced to compensate for local sampling density variations. For every point in the sampling set, we associate a small surrounding area. In case of the polar grid, we choose small ring segments. The area of such a ring segment around 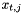 (
( 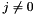 ) is
) is
![\[ w_{t,j} = \frac{\pi}{2TR^2}\left(\left(|j|+\frac{1}{2}\right)^2- \left(|j|-\frac{1}{2}\right)^2\right) = \frac{\pi |j| }{TR^2}\, . \]](form_129.png)
The area of the small circle of radius 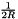 around the origin is
around the origin is 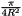 . Divided by the multiplicity of the origin in the sampling set, we get
. Divided by the multiplicity of the origin in the sampling set, we get 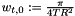 . Thus, the sum of all weights is
. Thus, the sum of all weights is 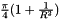 and we divide by this value for normalization.
and we divide by this value for normalization.
Definition at line 78 of file polar_fft_test.c.
References PI.
Referenced by inverse_polar_fft(), main(), polar_dft(), and polar_fft().