

|
3.2.3 |
Functions | |
| static int | mpolar_grid (int T, int R, double *x, double *w) |
Generates the points 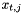 with weights with weights 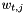 for the modified polar grid with for the modified polar grid with 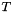 angles and angles and 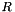 offsets. offsets. | |
| static int | mpolar_dft (fftw_complex *f_hat, int NN, fftw_complex *f, int T, int R, int m) |
| discrete mpolar FFT | |
| static int | mpolar_fft (fftw_complex *f_hat, int NN, fftw_complex *f, int T, int R, int m) |
| NFFT-based mpolar FFT. | |
| static int | inverse_mpolar_fft (fftw_complex *f, int T, int R, fftw_complex *f_hat, int NN, int max_i, int m) |
| inverse NFFT-based mpolar FFT | |
| static int | comparison_fft (FILE *fp, int N, int T, int R) |
| Comparison of the FFTW, mpolar FFT, and inverse mpolar FFT. | |
| int | main (int argc, char **argv) |
| test program for various parameters | |
Variables | |
| double | GLOBAL_elapsed_time |
|
static |
Generates the points 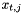 with weights
with weights 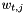 for the modified polar grid with
for the modified polar grid with 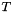 angles and
angles and 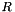 offsets.
offsets.
We add more concentric circles to the polar grid and exclude those nodes not located in the unit square, i.e.,
![\[ x_{t,j} := r_j\left(\cos\theta_t, \sin\theta_t\right)^{\top}\,,\qquad (j,t)^{\top}\in I_{\sqrt{2}R}\times I_T\,. \]](form_119.png)
with 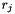 and
and 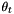 as for the polar grid. The number of nodes for the modified polar grid can be estimated as
as for the polar grid. The number of nodes for the modified polar grid can be estimated as 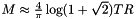 .
.
Definition at line 63 of file mpolar_fft_test.c.
References PI.
Referenced by inverse_mpolar_fft(), main(), mpolar_dft(), and mpolar_fft().